Fiche pédagogique n°05b :

Formulaires de calcul de la parallaxe solaire

J.-E. Arlot, P. Rocher (IMCCE) jeudi 20 mai 2004

I.Introduction

Dans cette fiche nous allons donner des formulaires simples permettant de calculer une approximation de la parallaxe solaire à partir de deux observations faites depuis des lieux éloignés. Attention, le choix des deux lieux d’observation peut être optimisé. Nous vous conseillons de consulter la fiche n°05c avant de choisir un partenaire à l’autre bout du monde…

Vous trouverez ci-dessous deux types de formulaires :

Un formulaire utilisant deux observations de contacts entre Vénus et le disque solaire. Attention, les deux observations doivent concerner le même type d’événement : soit les premiers contacts extérieurs, soit les premiers contacts intérieurs, soit les derniers contacts intérieurs, soit les derniers contacts extérieurs. On ne peut associer des événements différents. Cette méthode nécessite de disposer d’une bonne horloge en Temps Universel, ou, du moins, de disposer de la même échelle de temps pour les deux observations. Elle correspond à la méthode de Delisle.

Un formulaire utilisant les durées de passage observées. De même, on considérera deux durées séparant les mêmes types de contacts : soit entre les contacts extérieurs (difficile), soit entre les contacts intérieurs. Cette méthode ne nécessite pas d’horloge absolue, mais seulement la mesure précise d’une durée. Elle nécessite cependant que les deux lieux d’observation puissent observer le début et la fin du passage. Elle correspond à la méthode de Halley.

Coefficients pré-calculés

Pour obtenir ces formulaires, nous avons pré calculé des paramètres A, B et C qui ne dépendent pas de la position des observateurs mais qui rendent compte des mouvements de Vénus et de la Terre autour du Soleil ainsi que du mouvement de rotation de la Terre autour de son axe. Le paramètre dD/dt représente la variation instantanée de la distance du centre de Vénus au centre du Soleil. On peut donc ainsi effectuer un calcul de triangulation entre deux sites d’observation en tenant compte du fait que les observateurs et les centres de Vénus, de la Terre et du Soleil ne sont pas dans le même plan et en intégrant le rapport des distances au Soleil et à Vénus donné par la troisième loi de Képler.

Description du contact	A	B	C	dD/dt "/min
Premier contact extérieur (indice 1)	2,2606	-0,0194	1,0110	-3,0846
Premier contact intérieur (indice 2)	2,1970	0,2237	1,1206	-2,9394
Dernier contact intérieur (indice 3)	-1,0929	-1,1376	1,9090	2,9391
Dernier contact extérieur (indice 4)	-0,9799	-1,3390	1,8383	3,0842

Table n°1

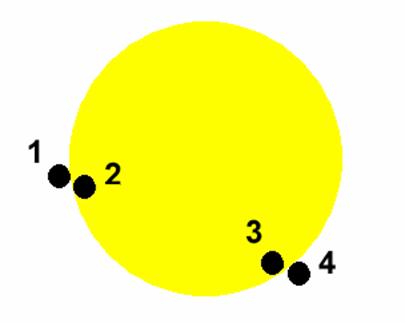
Contacts successifs entre Vénus et le Soleil

II Observation des contacts

Les données numériques dont vous devez disposer sont les suivants :

- latitudes et longitudes des deux lieux d’observation (l₁, j₁; l₂, j₂)

- les instants des contacts « i » (i=1, 2 , 3 ou 4) observés pour les lieux 1 et 2 dans la même échelle de temps -Temps Universel si possible- (t_i_,1 ; t_i_,2)

La formule est la suivante :

[A_i (cos j₁ cos l₁ – cos j₂ cos l₂) + B_i (cos j₁ sin l₁ – cos j₂ sin l₂)

+ C_i (sin j₁ – sin j₂)] p₀ = – dD/dt (t_i_,1 – t_i_,2)

Pour faire le calcul, remplissez la feuille de calcul “Delisle” ci-après.

III Observation des durées

Les données numériques dont vous devez disposer sont les suivants :

- latitudes et longitudes des deux lieux d’observation (l₁, j₁; l₂, j₂)

- la différence des durées DT observées depuis les deux lieux (durée lieu 1 – durée lieu 2) correspondant aux contacts « i et j » (i,j=1,4 pour les contacts extérieurs ou 2,3 pour les contacts intérieurs) observés pour les lieux 1 et 2

- La formule est la suivante :

[(Ai+Aj) (cos j₁ cos l₁ – cos j₂ cos l₂)

+ (Bi+Bj) (cos j₁ sin l₁ – cos j₂ sin l₂)

+ (Ci+Cj) (sin j₁ – sin j₂)] . p₀

= – DT . dD/dt

Pour faire le calcul, remplissez la feuille de calcul “Halley” ci-après.

Feuille de calcul « Delisle » :

calcul de la parallaxe solaire à l’aide de l’observation de contacts depuis deux lieux différents

Les données numériques dont vous devez disposer sont les suivants :

- latitudes et longitudes des deux lieux d’observation (l₁, j₁; l₂, j₂)

- les instants des contacts « i » (i=1, 2 , 3 ou 4) observés pour les lieux 1 et 2 dans la même échelle de temps -Temps Universel si possible- (t_i_,1 ; t_i_,2)

La formule (F1) est la suivante :

[A_i (cos j₁ cos l₁ – cos j₂ cos l₂)

+ B_i (cos j₁ sin l₁ – cos j₂ sin l₂)

+ C_i (sin j₁ – sin j₂)] p₀

= – dD/dt (t_i_,1 – t_i_,2)

Pour faire le calcul, remplissez la feuille de calcul “Delisle” ci-après. Attention, une feuille pour deux observations du même contact « i »

Longitude du lieu d’observation n°1 : l₁=

(1) Calculez le cosinus de l₁: cos (l₁) =

(2) Calculez le sinus de l₁: sin (l₁) =

Latitude du lieu d’observation n°1 :j₁ =

(3) Calculez le cosinus de j₁: cos (j₁) =

(4) Calculez le sinus de j₁: sin (j₁) =

Longitude du lieu d’observation n°2 : l₂=

(5) Calculez le cosinus de l₂: cos (l₂) =

(6) Calculez le sinus de l₂: sin (l₂) =

Latitude du lieu d’observation n°2 :j₂ =

(7) Calculez le cosinus de j₂: cos (j₂) =

(8) Calculez le sinus de j₂: sin (j₂) =

(9) Calculez (cos j₁ cos l₁) = ligne (3) x ligne (1) =

(10) Calculez (cos j₂ cos l₂) = ligne (7) x ligne (5) =

(11) Calculez (cos j₁ cos l₁ – cos j₂ cos l₂) = ligne (9) – ligne (10) =

(12) Calculez (cos j₁ sin l₁) = ligne (3) x ligne (2) =

(13) Calculez (cos j₂ sin l₂) = ligne (7) x ligne (6) =

(14) Calculez (cos j₁ sin l₁ – cos j₂ sin l₂) = ligne (12) – ligne (13) =

(15) Calculez (sin j₁ - sin j₂ ) = ligne (4) – ligne (8) =

Valeur de l’indice i pour ce calcul =

(16) Déterminez Ai à partir de la table n°1 =

(17) Déterminez Bi à partir de la table n°1 =

(18) Déterminez Ci à partir de la table n°1 =

On détermine maintenant la valeur numérique du premier membre de l’équation (F1) :

(19) Calculez Ai x ligne (11) =

(20) Calculez Bi x ligne (14) =

(21) Calculez Ci x ligne (15) =

(22) Calculez le premier membre de (F1) :

ligne (19) + ligne (20) + ligne (21) =

(23) Instant d’observation du contact « i » sur le lieu n°1 : t_i_,1 =

(24) Instant d’observation du contact « i » sur le lieu n°1 : t_i_,1 =

(25) Différence entre ces deux instants : (t_i_,1 – t_i_,2) =

(26) Conversion de cette différence en minutes et fraction de minute =

(27) Déterminez dD/dt à partir de la table n°1 : dD/dt =

(28) Calculez le deuxième membre de l’équation (F1) :

ligne (27) x ligne (26) x (-1) =

(29) Calculez p₀ = ligne (28) / ligne (22) =

(30) Rayon de la Terre = 6 378,1363 km

(31) Calculez l’unité astronomique :

UA = ligne (30) x 206265,806247 / ligne (29) =

Vous pouvez refaire le calcul pour chacun des contacts et moyenner les résultats

Formulaire « Halley » :

calcul de la parallaxe solaire à l’aide de l’observation de durées de passage depuis deux lieux différents

Les données numériques dont vous devez disposer sont les suivants :

- latitudes et longitudes des deux lieux d’observation (l₁, j₁; l₂, j₂)

- la durée DT de passage de Vénus pour chacun des lieux 1 et 2 correspondant aux contacts extérieurs (i=1, j=4) ou intérieurs (i=2, j=3)

- la différence des durées DT observées depuis les deux lieux (durée lieu 1 – durée lieu 2) correspondant aux contacts extérieurs (i=1, j=4) ou intérieurs (i=2, j=3)

La formule (F2) est la suivante :

[(Ai+Aj) (cos j₁ cos l₁ – cos j₂ cos l₂)

+ (Bi+Bj) (cos j₁ sin l₁ – cos j₂ sin l₂)

+ (Ci+Cj) (sin j₁ – sin j₂)] . p₀

= – DT . dD/dt

Longitude du lieu d’observation n°1 : l₁=

(1) Calculez le cosinus de l₁: cos (l₁) =

(2) Calculez le sinus de l₁: sin (l₁) =

Latitude du lieu d’observation n°1 :j₁ =

(3) Calculez le cosinus de j₁: cos (j₁) =

(4) Calculez le sinus de j₁: sin (j₁) =

Longitude du lieu d’observation n°2 : l₂=

(5) Calculez le cosinus de l₂: cos (l₂) =

(6) Calculez le sinus de l₂: sin (l₂) =

Latitude du lieu d’observation n°2 :j₂ =

(7) Calculez le cosinus de j₂: cos (j₂) =

(8) Calculez le sinus de j₂: sin (j₂) =

(9) Calculez (cos j₁ cos l₁) = ligne (3) x ligne (1) =

(10) Calculez (cos j₂ cos l₂) = ligne (7) x ligne (5) =

(11) Calculez (cos j₁ cos l₁ – cos j₂ cos l₂) = ligne (9) – ligne (10) =

(12) Calculez (cos j₁ sin l₁) = ligne (3) x ligne (2) =

(13) Calculez (cos j₂ sin l₂) = ligne (7) x ligne (6) =

(14) Calculez (cos j₁ sin l₁ – cos j₂ sin l₂) = ligne (12) – ligne (13) =

(15) Calculez (sin j₁ - sin j₂ ) = ligne (4) – ligne (8) =

Valeur des indices i et j pour ce calcul 1 et 4 pour une durée calculée à partir des contacts extérieurs ; 2 et 3 à partir des contacts intérieurs)

i =

j =

(16) Déterminez Ai à partir de la table n°1 =

(17) Déterminez Aj à partir de la table n°1 =

(18) Calculez Ai + Aj =

(19) Déterminez Bi à partir de la table n°1 =

(20) Déterminez Bj à partir de la table n°1 =

(21) Calculez Bi + Bj =

(22) Déterminez Ci à partir de la table n°1 =

(23) Déterminez Cj à partir de la table n°1 =

(24) Calculez Ci + Cj =

On détermine maintenant la valeur numérique du premier membre de l’équation (F1) :

(25) Calculez (Ai+Aj) x ligne (11) =

(26) Calculez (Bi+Bj) x ligne (14) =

(27) Calculez (Ci+Cj) x ligne (15) =

(28) Calculez le premier membre de (F2) :

ligne (25) + ligne (26) + ligne (27) =

(29) Durée du passage observé au lieu n°1 =

(30) Conversion de cette durée en minutes et fraction de minute =

(31) Durée du passage observé au lieu n°2 =

(32) Conversion de cette durée en minutes et fraction de minute =

(33) Différence de durées entre les deux lieux : DT = ligne (30) – ligne (32) =

(34) Déterminez dD/dt à partir de la table n°1 : dD/dt =

(35) Calculez le deuxième membre de l’équation (F2) :

ligne (33) x ligne (34) x (-1) =

(36) Calculez p₀ = ligne (35) / ligne (28) =

(37) Rayon de la Terre = 6 378,1363 km

(38) Calculez l’unité astronomique :

UA = ligne (37) x 206265,806247 / ligne (36) =

Vous pouvez refaire le calcul pour chacun des contacts et moyenner les résultats

On rappelle que ces méthodes ne sont pas exactes, et que l’on doit utiliser des formules plus complexes pour réduire les observations.